Engineering Mathematics GATE-2007

Q 1: Given i=\sqrt{-1} , the ratio \left(\frac{i+3}{i+1}\right) is given by

A) i
B) -2
C) -i+2
D) i+1

Show Answer

Q 2: The value of ‘a’ for which the following set of equations

y+2z=0
2x+y+z=0
ax+2y=0

have a non-trivial solution, is

A) 0
B) 8
C) -2
D) 3

Show Answer

Q 3: The initial condition for which the following equation

(x^2+2x)\frac{dy}{dx}=2(x+1)y;\;\;y(x_0)=y_0

has infinitely many solutions, is

A) y(x=0) = 5
B) y(x=0) = 1
C) y(x=2) = 1
D) y(x=-2) = 0

Show Answer

Q4: Given that the Laplace transform of the function below over a single period 0 < t < 2 is \frac1{s^2}\left(1-e^{-s}\right)^2 , the Laplace transform of the periodic function over 0 < t < ∞ is

A) \frac1s(1-e^{s})^2
B) \frac1s(1-e^{-s})^2
C) \frac{1\left(1-e^{-s}\right)}{s^2\left(1+e^{-s}\right)}
D) \frac1s\tanh\frac s2

Show Answer

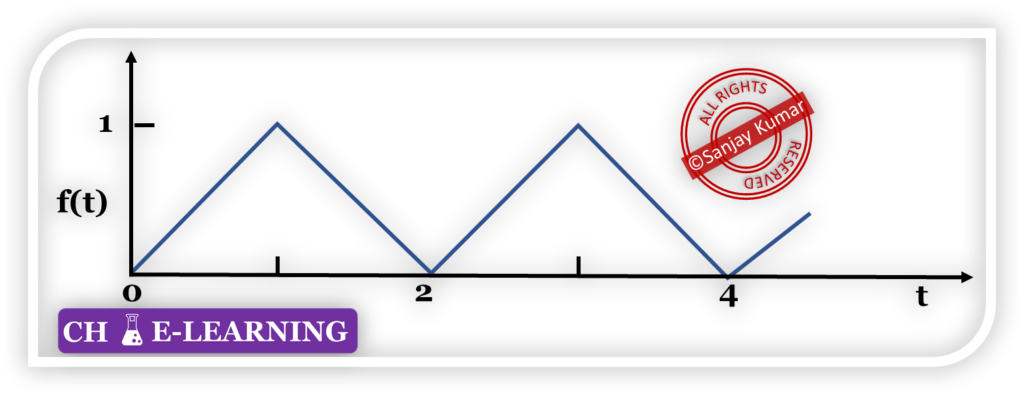
Q 5: If z=x+iy is a complex number, where i=\sqrt{-1} then the derivative of z\overline z at 2 + i is

A) 0
B) 2
C) 4
D) does not exist

Show Answer

Q 6: \overset=A and \overset=B are two 3×3 matrix such that \overset=A=\begin{bmatrix}-2&4&6\\1&2&1\\0&4&4\end{bmatrix} , \overset=B=\overset=0 and \overset=A\overset=B=\overset=0 . Then the rank of matrix \overset=B is

A) r = 2
B) r < 3
C) r ≤ 3
D) r = 3

Show Answer

Q 7: The solution of the following differential equation x\frac{dy}{dx}+y(y^2-1)=2x^3 is

A) 0
B) 2+ce^{-x^2/2}
C) c_1x+c_2x^2
D) 2x+cxe^{-x^2/2}

Show Answer

Q 8: The directional derivative of f=\frac12\sqrt{x^2+y^2} at (1, 1) in the direction of \overrightarrow b=\overrightarrow i-\overrightarrow j is

A) 0
B) 1/\sqrt2
C) \sqrt2
D) 2

Show Answer

Q 9: Evaluate the following integral (n ≠ 0) \int_c\left(-xy^ndx+x^nydy\right) within the area of a triangle with vertices (0, 0), (1, 0) and (1, 1) (counter-clockwise).

A) 0
B) 1/(n+1)
C) 1/2
D) n/2

Show Answer

Q 10: The family of curves that is orthogonal to xy = c is

A) y=c_1x
B) y=c_1/x
C) y^2+x^2=c_1
D) y^2-x^2=c_1

Show Answer

Q 11: The Laplace transform of f(t)=1/\sqrt t is

A) \sqrt{\frac{\mathrm\pi}s}
B) \frac1{\sqrt s}
C) \frac1{s^{3/2}}
D) does not exist

Show Answer

Q 12: The thickness of a conductive coating in micrometers has a probability density function of 600x^{-2} for 100 μm < x < 120 μm. The mean and the variance of the coating thickness is

A) 1 μm, 108.39 μm²
B) 33.83 μm, 1 μm²
C) 105 μm, 11 μm²
D) 109.39 μm, 33.83 μm²

Show Answer